|
Марковский случайные процесс с дискретными состояниями и дискретным временем называют Марковской цепью. Для такого процесса моменты 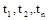 , когда система , когда система 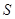 может менять свое состояние, рассматривают как последовательные шаги процесса, а в качестве аргумента, от которого зависит процесс, выступает не время t, номер шага 1, 2, …, k, … Случайный процесс в этом случае характеризуется последовательностью состояний может менять свое состояние, рассматривают как последовательные шаги процесса, а в качестве аргумента, от которого зависит процесс, выступает не время t, номер шага 1, 2, …, k, … Случайный процесс в этом случае характеризуется последовательностью состояний 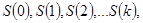 где где 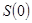 - начальное состояние системы (перед первым шагом); - начальное состояние системы (перед первым шагом); 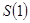 - состояние системы после первого шага; - состояние системы после первого шага; 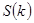 - состояние системы после k-го шага… - состояние системы после k-го шага…
Событие 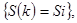 состояние в том, что сразу после k-го шага система находится в состоянии состояние в том, что сразу после k-го шага система находится в состоянии 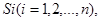 является случайным событием. Последовательность состояний является случайным событием. Последовательность состояний 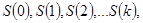 можно рассматривать как последовательность случайных событий. Такая случайная последовательность событий называется Марковской цепью, если для каждого шага вероятность перехода из любого состояния можно рассматривать как последовательность случайных событий. Такая случайная последовательность событий называется Марковской цепью, если для каждого шага вероятность перехода из любого состояния 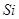 в любом в любом 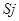 не зависит от того, когда и как система пришла в состояние не зависит от того, когда и как система пришла в состояние 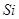 . Начальное состояние . Начальное состояние 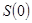 может быть заданием заранее или случайным. может быть заданием заранее или случайным.
Вероятностями состояний цепи Маркова называются вероятности 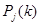 того, что после k-го шага (и до (k+1) - го) система того, что после k-го шага (и до (k+1) - го) система 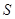 будет находиться в состоянии будет находиться в состоянии 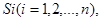 . Очевидно, для любого k . Очевидно, для любого k
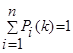
Начальным распределением вероятностей Марковской цепи называется распределение вероятностей состояний в начале процесса:
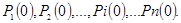
В частном случае, если первоначальное состояние системы S в точности известно 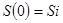 , то начальная вероятность , то начальная вероятность 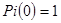 , а все остальные равны нулю. Вероятность перехода на k-м шаге из состояния , а все остальные равны нулю. Вероятность перехода на k-м шаге из состояния 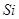 в состояние в состояние 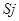 при условии, что непосредственно перед этим она находится в состоянии при условии, что непосредственно перед этим она находится в состоянии 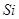 . .
Поскольку система может пребывать в одном из n состояний, то для каждого момента времени 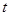 необходимо задать необходимо задать 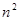 вероятностей перехода вероятностей перехода 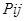 , которое удобно представить в виде следующей матрицы: , которое удобно представить в виде следующей матрицы:
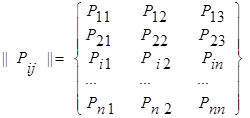
где 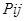 - вероятность перехода за один шаг из состояния - вероятность перехода за один шаг из состояния 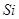 в состояние в состояние 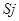 . .
Матрица называется переходной или матрицей переходных вероятностей.
Если переходные вероятности не зависят от номера шага, а зависят только от того, из какого состояния в какое осуществляется переход, то соответствующая цепь Маркова называется однородной.
Переходные вероятности однородной Марковской цепи 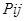 образуют квадратную матрицу размера образуют квадратную матрицу размера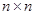 . Отметим некоторые ее особенности: . Отметим некоторые ее особенности:
1. Каждая строка характеризует выбранное состояние системы, а ее элементы представляют собой вероятности всех возможных переходов за один шаг из выбранного состояния, в том числе и переход в самое себя.
2. Элементы столбцов показывают вероятности всех возможных переходов системы за один шаг в заданное состояние (иначе говоря, строка характеризует вероятность перехода системы из состояния, столбец - в состояние).
3. Сумма вероятностей каждой строки равна единице, так как переходы образуют полную группу несовместных событий:
|