|
Среднечастотный участок. Для заданного значения 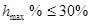 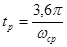 , откуда частота среза для желаемой ЛАХ , откуда частота среза для желаемой ЛАХ 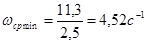 . Так как при наличии начального рассогласования . Так как при наличии начального рассогласования 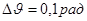 , ускорения выходной координаты ограничивается значением 10 рад/с , ускорения выходной координаты ограничивается значением 10 рад/с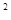 , то частота среза должна быть не более, чем , то частота среза должна быть не более, чем 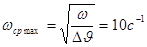 . .
Следовательно, частоту среза для желаемой ЛАХ выбираем в диапазоне: 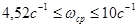 . .
Зададимся 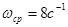 . Определяем частоты, ограничивающие среднечастотную асимптоту справа . Определяем частоты, ограничивающие среднечастотную асимптоту справа 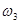 и слева и слева 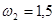 . Хорошие динамические свойства обеспечиваются в случае, если выполняются условия: . Хорошие динамические свойства обеспечиваются в случае, если выполняются условия:
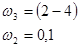 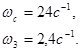
Среднечастотный участок обычно равен как минимуму интервалу частот в одну декаду.
Низкочастотный участок. Определяет точность работы САУ в установившемся режиме или ее статические свойства.
Исходя из требований к точности АС в установившемся режиме (заданного коэффициента разомкнутой системы 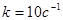 ), порядка астатизма ), порядка астатизма 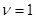 проводим низкочастотную асимптоту желаемой ЛАХ проводим низкочастотную асимптоту желаемой ЛАХ 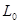 с наклоном - 20 дБ/дек через точку с координатами с наклоном - 20 дБ/дек через точку с координатами 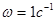 , ,  . Протяженность . Протяженность 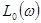 устанавливаем, исходя из необходимого запаса устойчивости по амплитуде устанавливаем, исходя из необходимого запаса устойчивости по амплитуде 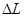 , т.е. не менее 13 дБ. , т.е. не менее 13 дБ.
Среднечастотную и низкочастотную части сопрягаем под наклоном -40 дБ/дек, т. е. таким образом, чтобы было наименьшее число изломов асимптотической желаемой ЛАХ.
Высокочастотная часть не влияет ни на устойчивость, ни на качество, поэтому ее проводим под таким же наклоном, как и у неизменяемой системы. Таким образом, получаем желаемую ЛАХ, передаточная функция которой имеет вид:
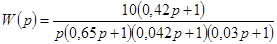 . .
Далее, определяем передаточную функцию замкнутой системы 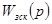 и проверяем ее на устойчивость по критерию Гурвица. и проверяем ее на устойчивость по критерию Гурвица.
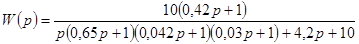 . .
Характеристическое уравнение замкнутой системы имеет вид:
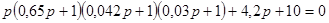
Тогда а0=10; a1=5,2; a2=0,722; a3= 0,0483; a4= 0,000819. Для устойчивости системы необходимо и достаточно, чтобы при аi > 0 все определители Гурвица были больше 0. При положительности всех коэффициентов характеристического уравнения для устойчивости системы требуется выполнение условия:
a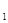 (a (a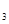 a a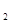 - a - a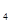 a a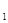 ) - а ) - а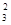 ∙а ∙а > 0 > 0
0,15 > 0. Следовательно, система устойчива.
|