|
) Найдем цены альтернатив:
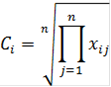
|
С1 |
5,2 | |
С2 |
0,57 | |
С3 |
0,51 | |
С4 |
0,97 | |
С5 |
0,42 | |
С6 |
0,77 | |
С7 |
1,04 | |
С8 |
0,86 | |
С9 |
1,94 | |
С10 |
1,16 | |
С11 |
0,54 | |
С12 |
1,03 |
2) Найдем суммы цен альтернатив:
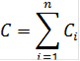
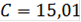
3) Найдем веса альтернатив:
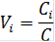
|
V1 |
0,346436 | |
V2 |
0,037975 | |
V3 |
0,033977 | |
V4 |
0,064624 | |
V5 |
0,027981 | |
V6 |
0,051299 | |
V7 |
0,069287 | |
V8 |
0,057295 | |
V9 |
0,129247 | |
V10 |
0,077282 | |
V11 |
0,035976 | |
V12 |
0,068621 |
Наиболее предпочтительной альтернативой является та, у которой максимальный вес. В данном случае это альтернатива А1.
) Возможна проверка оценок на непротиворечивость. Она позволяет выявить ошибки, которые может допустить эксперт при заполнении матрицы сравнений.
Оценка на непротиворечивость:
) Находим сумму столбцов матрицы парных сравнений:
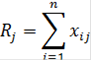
|
R1 |
72 | |
R2 |
19,97 | |
R3 |
27,89 | |
R4 |
29,82 | |
R5 |
21,22 | |
R6 |
26,54 | |
R7 |
35,53 | |
R8 |
29,22 | |
R9 |
53,06 | |
R10 |
34,07 | |
R11 |
20,2 | |
R12 |
33,89 |
Перейти на страницу: 1 2 3 |